
Fluid Mechanics
Fluids
Fluids are those substances which can flow when an external force is applied on it.
Liquids and gases are fluids.
Fluids do not have finite shape but takes the shape of the containing vessel,
The total normal force exerted by liquid at rest on a given surface is called thrust of liquid.
The SI unit of thrust is newton.
In fluid mechanics the following properties of fluid would be considered
(i) When the fluid is at rest – hydrostatics
(ii) When the fluid is in motion – Fluid Mechanics
Pressure Exerted by the Liquid
The normal force exerted by a liquid per unit area of the surface in contact is called pressure of liquid or hydrostatic pressure.
Pressure exerted by a liquid column
p = hρg
Where, h = height of liquid column, ρ = density of liquid
and g = acceleration due to gravity
Mean pressure on the walls of a vessel containing liquid upto height h is (hρg / 2).
Pascal’s Law
The increase in pressure at a point in the enclosed liquid in equilibrium is transmitted equally in all directions in liquid and to the Walls of the container.
The working of hydraulic lift, hydraulic press and hydraulic brakes are based on Pascal’s law.
Atmospheric Pressure
The pressure exerted by the atmosphere on earth is atmospheric pressure.
It is about 100000 N/m2.
It is equivalent to a weight of 10 tones on 1 m2.
At sea level, atmospheric pressure is equal to 76 cm of mercury column. Then, atmospheric pressure
= hdg = 76 x 13.6 x 980 dyne/cm2
[The atmospheric pressure does not crush our body because the pressure of the blood flowing through our circulatory system] balanced this pressure.]
Atmospheric pressure is also measured in torr and bar.
1 torr = 1 mm of mercury column
1 bar = l05 Pa
Aneroid barometer is used to measure atmospheric pressure.
Buoyancy
When a body is partially or fully immersed in a fluid an upward force acts on it, which is called buoyant force or simply buoyancy.
The buoyant force acts at the centre of gravity of the liquid displaced] by the immersed part of the body and this point is called the centre buoyancy.
Archimedes’ Principle
When a body is partially or fully immersed in a liquid, it loses some of its weight. and it is equal to the weight of the liquid displaced by the immersed part of the body.
If T is the observed weight of a body of density σ when it is fully immersed in a liquid of density p, then real weight of the body
w = T / ( 1 – p / σ)
Laws of Floatation
A body will float in a liquid, if the weight of the body is equal to the weight of the liquid displaced by the immersed part of the body.
If W is the weight of the body and w is the buoyant force, then
(a) If W > w, then body will sink to the bottom of the liquid.
(b) IfW < w, then body will float partially submerged in the liquid.
(c) If W = w, then body will float in liquid if its whole volume is just immersed in the liquid,
The floating body will be in stable equilibrium if meta-centre (centre of buoyancy) lies vertically above the centre of gravity of the body.
The floating body will be in unstable equilibrium if meta-centre (centre of buoyancy) lies vertically below the centre of gravity of the body.
The floating body will be in neutral equilibrium if meta-centre (centre of buoyancy) coincides with the centre of gravity of the body.
Density and Relative Density
Density of a substance is defined as the ratio of its mass to its volume.
Density of a liquid = Mass / Volume
Density of water = 1 g/cm3 or l03 kg/m3
It is scalar quantity and its dimensional formula is [ML-3].
Relative density of a substance is defined as the ratio of its density to the density of water at 4°C,
Relative density = Density of substance / Density of water at 4°C
= Weight of substance in air / Loss of weight in water
Relative density also known as specific gravity has no unit, no dimensions.
For a solid body, density of body = density of substance
While for a hollow body, density of body is lesser than that of Substance.
When immiscible liquids of different densities are poured in a container, the liquid of highest density will be at the bottom while, that of lowest density at the top and interfaces will be plane.
Density of a Mixture of Substances
When two liquids of mass m1 and m2 having density p1 and p2 are mixed together then density of mixture is
p = m1 + m2 / (m1 /p1 ) + (m2 + p2)
= p1p2 (m1 + m2) / (m1p2 + m2p1)
When two liquids of same mass m but of different densities p1 and p2 are mixed together then density of mixture is
p = 2p1p2 / p1 + p2
When two liquids of same volume V but of different densities p1 and p2 are mixed together then density of mixture is
p = p1 + p2 / 2
Density of a liquid varies with pressure
p = po [ 1 + Δp / K]
where, po = initial density of the liquid, K = bulk modulus of elasticity of the liquid and Δp = change in pressure.
Viscosity
The property of a fluid by virtue of which an internal frictional force acts between its different layers which opposes their relative motion is called viscosity.
These internal frictional force is called viscous force.
Viscous forces are intermolecular forces acting between the molecules of different layers of liquid moving with different velocities.
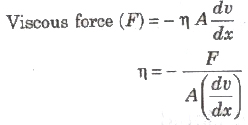
where, (dv/dx) = rate of change of velocity with distance called velocity gradient, A = area of cross-section and = coefficient of viscosity.
SI unit of η is Nsm-2 or pascal-second or decapoise. Its dimensional formula is [ML-1T-1].
The knowledge of the coefficient of viscosity of different oils and its variation with temperature helps us to select a suitable lubricant for a given machine.
Viscosity is due to transport of momentum. The value of viscosity (and compressibility) for ideal liquid is zero.
The viscosity of air and of some liquids is utilised for damping the n.ving parts of some instruments.
The knowledge of viscosity of some organic liquids is used in determining the molecular weight and shape of large organic moleculars like proteins and cellulose.
Variation of Viscosity
The viscosity of liquids decreases with increase in temperature
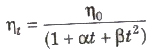
where, η0 and ηt is are coefficient of viscosities at 0°C t°C, α and β are constants.
The viscosity of gases increases with increase in temperatures as
η ∝ √T
The viscosity of liquids increases with increase in pressure but the viscosity of water decreases with increase in pressure.
The viscosity of gases do not changes with pressure.
Poiseuille’s Formula
The rate of flow (v) of liquid through a horizontal pipe for steady flow is given by

where, p = pressure difference across the two ends of the tube. r = radius of the tube, n = coefficient of viscosity and 1 = length of th tube.
The Rate of Flow of Liquid
Rate of flow of liquid through a tube is given by
v = (P/R)
where, R = (8 ηl/πr4), called liquid resistance and p = liquid pressure.
(i) When two tubes are connected in series
(ii) When two tubes are connected in parallel
Stoke’s Law
When a small spherical body falls in a long liquid column, then after sometime it falls with a constant velocity, called terminal velocity. When a small spherical body falls in a liquid column with terminal velocity then viscous force acting on it is
F = 6πηrv
where, r = radius of the body, V = terminal velocity and η = coefficient of viscosity.
This is called Stoke’s law.

where,
Importance of Stoke’s Law
Flow of Liquid
Critical Velocity
The critical velocity is that velocity of liquid flow, below which its fl is streamlined and above which it becomes turbulent.
Critical velocity vc = (kη/rρ)
where,
Reynold’s Number
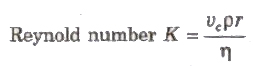
Reynold’s number is a pure number and it is equal to the ratio of inertial force per unit area to the viscous force per unit area for flowing fluid.
where, p = density of the liquid and vc = critical velocity.
For pure water flowing in a cylindrical pipe, K is about 1000.
When 0< K< 2000, the flow of liquid is streamlined.
When 2000 < K < 3000, the flow of liquid is variable betw streamlined and turbulent.
When K > 3000, the flow of liquid is turbulent.
It has no unit and dimension.
Equation of Continuity
If a liquid is flowing in streamline flow in a pipe of non-unif cross-section area, then rate of flow of liquid across any cross-sec remains constant.
a1v1 = a2v2 av = constant
The velocity of liquid is slower where area of cross-section is larger faster where area of cross-section is smaller.
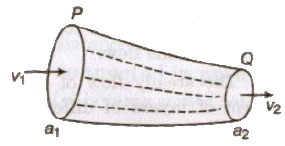
The falling stream of water becomes narrower, as the velocity of f stream of water increases and therefore its area of cross-s decreases.
Energy of a Liquid
A liquid in motion possess three types of energy
(i) Pressure Energy Pressure energy per unit mass = p/ρ
where,
p= pressure of the liquid and p = density of the liquid.
Pressure energy per unit volume = p
(ii) Kinetic Energy
(iii) Potential Energy
Bernoulli’s Theorem
If an ideal liquid is flowing in streamlined flow then total energy, i.e., sum of pressure energy, kinetic energy and potential energy per unit
volume of the liquid remains constant at every cross-section of the tube.
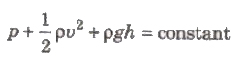
Mathematically
It can be expressed as
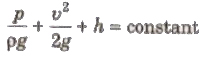
where, (p/ρg) = pressure head, (v2/2g) = velocity head and h = gravitational head.
For horizontal flow of liquid,

Applications of Bernoulli’s Theorem
Venturimeter
It is a device used for measuring the rate of flow of liquid t pipes. Its working is based on Bernoulli’s theorem.
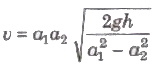
Rate of flow of liquid,
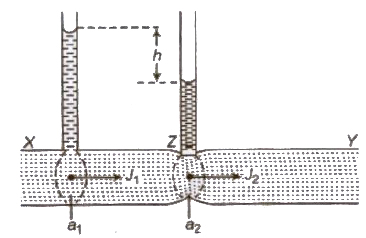
where, a1 and a2 are area of cross-sections of tube at bra and narrower part and h is difference of liquid columns in ver tubes.
Torricelli’s Theorem
Velocity of efflux (the velocity with which the liquid flows out orifice or narrow hole) is equal to the velocity acquired by a falling body through the same vertical distance equal to the dep orifice below the free surface of liquid.

Velocity of efflux, v = √2gh
where, h = depth of orifice below the free surface of liquid.
Horizontal range, S = √4h(H — h)
where, H = height of liquid column.
Horizontal range is maximum, equal to height of the liquid column H, when orifice is at half of the height of liquid column.
Important Points
Surface tension is the property of any liquid by virtue of which tries to minimize its free surface area.
Surface tension of a liquid is measured as the force acting per length on an imaginary line drawn tangentially on the free surface the liquid.
Surface tension S = Force/Length = F/l = Work done/Change in area
Its SI unit is Nm-1 or Jm-2 and its dimensional formula is [MT-2].
It is a scalar quantity. Surface tension is a molecular phenomenon which is due to cohesive force and root cause of the force is electrical in nature.
Surface tension of a liquid depends only on the nature of liquid and independent of the surface area of film or length of the line .
Small liquid drops are spherical due to the property of surface tension.
Adhesive Force
The force of attraction acting between the molecules of different substances is called adhesive force, e.g., the force of attracts acting between the molecules of paper and ink, water and glass, etc.
Cohesive Force
The force of attraction acting between the molecules of same substan is called cohesive force. e.g., the force of attraction acting between molecules of water, glass, etc.
Cohesive forces and adhesive forces are van der Waals’ forces.
These forces varies inversely as the seventh power of distance between the molecules.
Molecular Range
The maximum distance upto which a molecule can exert a force of attraction on other molecules is called molecular range.
Molecular range is different for different substances. In solids and liquids it is of the order of 10-9 m.
If the distance between the molecules is greater than 10-9 m, the force of attraction between them is negligible.
Surface Energy
If we increase the free surface area of a liquid then work has to be done against the force of surface tension. This work done is stored in liquid stu-face as potential energy,
This additional potential energy per unit area of free surface of liquid is called surface energy.
Surface energy (E) = S x &ΔM
where. S = surface tension and ΔA = increase in surface area.
(i) Work Done in Blowing a Liquid Drop If a liquid drop is blown up from a radius r1 to r2 then work done for that is
W = S . 4π (r22 – r12)
(ii) Work Done in Blowing a Soap Bubble As a soap bubble has two free surfaces, hence work done in blowing a soap bubble so as to increase its radius from r1 to r2 is given by
W = S.8π(r22 – r12)
(iii) Work Done in Splitting a Bigger Drop into n Smaller Droplets
If a liquid drop of radius R is split up into n smaller droplets, all of same size. then radius of each droplet
r = R. (n)-1/3
Work done, W = 4π(nr2 – R2)
= 4πSR2 (n1/3 – 1)
(iv) Coalescance of Drops If n small liquid drops of radius reach combine together so as to form a single bigger drop of radius R=n1/3.r, then in the process energy is released. Release of energy is given by
ΔU = S.4π(nr2 – R2)
= 4πSπn(1 – n1/3)
Angle of Contact
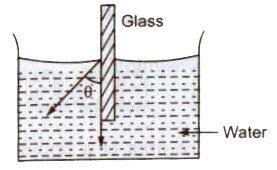
The angle subtended between the tangents drawn at liquid surface at solid surface inside the liquid at the point of contact, is called of contact (9).
Angle of contact depends upon the nature of the liquid and solid contact and the medium which exists above the free surface of liquid.
When wax is coated on a glass capillary tube, it becomes water-proof.
The angle of contact increases and becomes obtuse. Water does not in it. Rather it falls in the tube by virtue of obtuse angle of contact.
If θ is acute angle, i.e; θ <90°, then liquid meniscus will be concave upwards.
Angle of contact increases with increase in temperature of Angle of contact decreases on adding soluble impurity to a liquid.
Angle of contact for pure water and glass is zero. For ordinary water and glass is 8°. For mercury and glass is 140°. For pure water silver is 90°. For alcohol and clean glass θ = 0°.
Angle of contact, meniscus, shape of liquid surface


Capillarity
The phenomenon called capillarity. of rise or fall of liquid column in a capillary tube is Ascent of a liquid column in a capillary tube is given by
h = (2S cos θ / rρg) – (r / 3)
If capillary is very narrow, then
h=2S cos θ / rρg
where, r = radius of capillary tube, p = density of the liquid, and
θ = angle of contact and S = surface tension of liquid.
Some Practical Examples of Capillarity
Zurin’s Law
If a capillary tube of insufficient length is placed vertically in a then liquid never come out from the tube its own, as
Rh = constant ⇒ R1h1 = R2h2
where, R = radius of curvature of liquid meniscus and
h = height of liquid column.
When a tube is kept in inclined position in a liquid the vertical height remains unchanged then length of liquid column.

Liquid rises (water in glass capillary) or falls (mercury in capillary) due to property of surface tension
T = Rρgh / 2 cos θ
where, R = radius of capillary tube, h = height of liquid, p = density of liquid, e = angle of contact,
T = surface tension of liquid and 9 = acceleration due to gravity.
Excess Pressure due to Surface Tension
(i) Excess pressure inside a liquid drop = 2S / R
(ii) Excess pressure inside an air bubble in a liquid = 2S / R
(iii) Excess pressure inside a soap bubble = 4S / R
where, S = surface tension and R = radius of drop/bubble.
(iv) Work done in spraying a liquid drop of radius R into n droplets of radius r = T x increase in surface area
= 4πTR3 (1/r – 1/R)
Fall in temperature
Δθ = 3T/J (1/r – 1/R)
where. J = 4.2 J/cal.
(v) When n small drops are combined into a bigger drop, then work done is given by
W = 4πR2T (n 1/3 – 1)
Temperature increase
Δθ = 3T/J (1/r – 1/R)
(vi) When two bubbles of radii r1 and r2 coalesce into a bubble of radius r isothermally, then
r2 = r12 + r22
(vii) When two soap bubbles of radii ‘1 and ‘2 are in contact with each other, then radius (r) of common interface.

Factors Affecting Surface Tension
When charge is given to a soap bubble, its size increases surface tension of the liquid decreases due to electrification.
In weightlessness condition liquid does not rise in a capillary tube.
Some Phenomena Based on Surface Tension
Others Class 11 Physics Chapters:-















