
Transmission of Heat
Heat transfer is the physical phenomenon for which energy is transferred between any two particles of matter that are at different temperatures. There are three modes of heat transfer considered in the following: conduction, convection and radiation.
Methods of Heat Transmission
There are three methods of heat transmission
(i) Conduction In solids, heat is transmitted from temperature to lower temperature without actual movements the particles. This mode of transmission of heat. is conduction.
(ii) Convection The process of heat-transmission in which particles of the fluid (liquid or gas) move. is called convection. Land breeze and see-breeze are formed due to convection.
(iii) Radiation The process of heat transmission in the form electromagnetic waves, is called radiation.
Radiation do not require any medium for propagation.
It propagates without heating the intervening medium.
The heat energy transferred by radiation, is called energy.
Heat from the sun reaches the earth by radiation.
Thermal Conductivity
In solids, heat is transferred through conduction. We will conduction of heat through a solid bar.
Conduction of Heat in a Conducting Rod
Steady State
The state of a conducting rod in which no part of the rod absorbs nea is caned the steady state.
Isothermal Surface
A surface of a material whose all points are at the same temperature, is called an isothermal surface.
Temperature Gradient
The rate of change of temperature with distance between two isothermal surfaces is called temperature gradient.
Temperature gradient = Change in temperature / Perpendicular distance = – Δθ / Δx
Its SI unit is ‘oC per meter’ and dimension is [L-1θ].
The amount of heat flow in a conducting rod
Q = KA Δθt / l
where K = coefficient of thermal conductivity.
A = area of cross-section,
l = length of rod,
Δθ = temperature difference between the ends of the rod and
t = time.
The SI unit of K is ‘Wm-1 K-1‘ and its dimension is [MLT-3θ-1].
The value of K is large for good conductors and very small for insulators.
Thermal resistance is given by
R = Δθ / H = l / KA
where, Δθ is temperature difference at the ends of the rod and H rate of flow of heat.
Its SI unit is K/W and its dimensional formula is [ML2 T-3θ-1].
When Conducting Rods are Connected in Series
The amount of heat flow
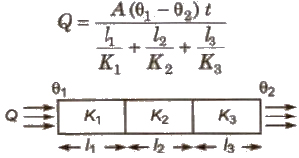
Equivalent thermal conductivity
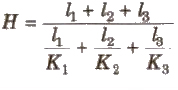
When Two Conducting Rods are Connected in Series
Rate of heat flow
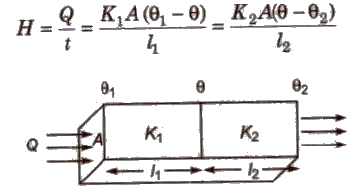
Temperature of contact surface
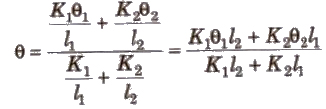
Equivalent thermal conductivity H = l1 + l2 / l1 / K1 + l2 / k2
Equivalent thermal resistance R = R1 + R2
When Conducting Rods are Connected in Parallel
Rate of heat flow
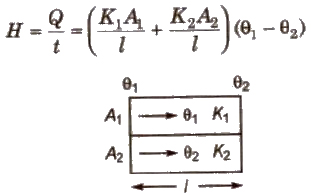
Equivalent thermal conductivity
K = K1 A1 + K2 A2 / A1 + A2
Equivalent thermal resistance
1 / R = 1 / R1 + 1 / R2
Ingen-Hausz Experiment
The thermal conductivities of different materials are proportional to the square of the lengths of the melted wax on the rods of these materials in the steady state.
If l1, l2, l3,…. are the lengths of the melted wax on the rods of different materials having coefficient of thermal conductivities K1, K2, K3,…, then
K1 : K2 : K3 :…. = l12 : l22 : l32 :….
or K1 / K2 = l12 / l22
Formation of Ice on Lakes
Time taken to form x thickness of ice on lake
t = (ρL / 2Kθ) x2
where ρ density of ice, L = latent heat of freezing of ice.
K = coefficient of thermal conductivity of ice and
θ = temperature above lake.
Time taken to increase the thickness of ice from x1 to x2
t = (ρ L / 2Kθ) (x22 – x21)
Reflectance or Reflecting Power
The ratio of the amount of thermal radiations reflected by a body in a given time to the total amount of thermal radiations incident on the body in that time is called reflectance or reflecting power of the body.
It is denoted by r.
Absorptance or Absorbing Power
The ratio of the amount of thermal radiations absorbed by a body in a given time to the total amount of thermal radiations incident on the body in that time, is called absorptance or absorbing power of the body.
It is denoted by a.
Transmittance or Transmitting Power
The ratio of the amount of thermal radiations transmitted by the body in a given time to the total amount of thermal radiations incident on the body in that time, is called transmittance or transmitting power of the body.
It is denoted by t.
Relation among reflecting power, absorbing power and transmitting power
r + a + t = l
If body does not transmit any heat radiations, then t = 0
∴ r + a = 1
(i) r, a and t all are the pure ratio, so they have no unit dimension.
(ii) For perfect reflector, r = 1, a = 0 and t = O.
(iii) For perfect absorber, a = 1, r = 0 and t = 0 (perfect black body).
(iv) For perfect transmitter, t = 1, a = 0 and r = O.
Emissive Power
Emissive power of a body at a particular temperature is the total amount of thermal energy emitted per unit time per unit area of thel body for all possible wavelengths.
It is denoted by eλ
Its SI unit is ‘joule sec-l metre-2 or ‘watt-metre-2‘.
Its dimensional formula is [MT-3].
Emissivity
Emissivity of a body at a given temperature is equal to the ratio of the total emissive power of the body (eλ) to the total emissive power of a perfectly black body (Eλ) at that temperature.
Emissivity ε = eλ / Eλ
Perfectly Black Body
A body which absorbs completely the radiations of all wavelengths incident on it, is called a perfectly black body.
For a perfectly black body, emissive power (Eλ) = 1
An ideal black body need not be black in colour.
The radiation from a black body depend upon its temperature only.
These heat radiations do not depend on density mass, size or the nature of the body.
Lamp black is 96% black and platinum black is about 98% black.
A perfectly black body cannot be realised in practice. The nearest example of an ideal black body is the Ferry’s black body.
Kirchhoff’s Law
The ratio of emissive power (eλ) to the absorptive power (aλ) cOrresponding to a particular wavelength and at any given temperature is always a constant for all bodies and it is equal to the emissive power (Eλ) of a perfectly black body at the same temperature and corresponding to the same wavelength.
Mathematically eλ / aλ = constant (Eλ)
Fraunhofer Lines
These are typical spectral absorption lines. These are dark but not perfectly black due to their lower intensity as compared to the remaining part of spectrum.
These lines are produced when a cold gas is in between a broad spectrum photon source and detector.
A set of several hundred dark lines appearing against the bright back ground of the continuous solar spectrum and produced by absorption of light by the cooler gases in the sun’s outer atmosphere at frequencies corresponding to the atomic transition frequencies of these gases.
About 20000 such dark lines have been detected so far. These dark lines belong to hydrogen, helium, sodium, iron, calcium etc.
Kirchhoff’s law explains this phenomenon.
Moon covers the photosphere the central part of sun at the time of total solar eclipse. Thus, the elements present in the chromosphere emit certain wavelength which they had absorbed. Because of this reason the Fraunhofer lines appears as bright lines at the time of total solar eclipse.
Variation of Colour with Temperature
(i) At temperature 525°e, the colour of object is red.
(ii) At temperature 900o e, the colour of object is cherry red.
(iii) At temperature 1100o e, the colour of object is orange red.
(iv) At temperature l200o e, the colour of object is yellow.
(v) At temperature l600o e, the colour of object is white.
Stefan’s Law
Heat energy emitted per second per unit area of a perfectly black body
E ∝ ⇒T4 ⇒ E = σ T4
where σ is Stefan’s constant and its value is 5.67 x 10-8 Wm-2 K-4.
If To is the temperature of the surroundings, then
E = σ (T4 – T4o)
If e is the emissivity of the body, then
E = ε σ T4
Energy radiated by whole body in t time,
E = σAt T4
Newton’s Law of Cooling
The rate of loss of heat of a liquid is directly proportional to difference in temperature of the liquid and its surroundings, i.e.
dT / dt = E ∝ (T – To)
where T and To are the temperatures of the liquid and surroundings.
Wien’s Displacement Law
For black body radiation the rate of energy radiation per unit area per unit wavelength range at constant kelvin temperature can be against wavelength.
λm T = constant (b)
where λm = wavelength corresponding to which maximum energy is radiated,
T = absolute temperature and
b = Wien’s constant = 2.898 x 10-3 = 3 X 10-3 mK
When temperature of a black body increases, colour changes towards higher frequency, i.e., from red → orange → yellow → green → blue → violet.
Solar Constant
The amount of heat received from the sun by one square centimetre area of a surface placed normally to the sun rays at mean distance the earth from the sun is known as solar constant. It is denoted by S.
S = (r / R)2 σ T4
Here, r is the radius of sun and R is the mean distance of earth from the centre of sun. Value of solar constant is 1.937 cal cm-2 min-1.
Temperature of violet star is maximum while temperature of red is minimum.
Others Class 11 Physics Chapters:-















