
Magnetism Class 12 Physics
The property of any object by virtue of which it can attract a piece of iron or steel is called magnetism.
Natural Magnet
A natural magnet is an ore of iron (Fe3O4), which attracts small pieces of iron, cobalt and nickel towards it.
Magnetite or lode stone is a natural magnet.
Artificial Magnet
A magnet which is prepared artificially is called an artificial magnet, e.g., a bar magnet, an electromagnet, a magnetic needle, a horse-shoe magnet etc.
According to molecular theory, every molecular of magnetic substance (whether magnetised or not) is a complete magnet itself.
The poles of a magnet are the two points near but within the ends of the magnet, at which the entire magnetism can be assumed to be concentrated.
The poles always occur in pairs and they are of equal strength. Like poles repel and unlike poles attract.
Properties of Magnet
(i) A freely suspended magnet always aligns itself into north-south direction.
(ii) Like magnetic poles repel and unlike magnetic poles attract each other.
(iii) Magnetic poles exist in pair.
Coulomb’s Law
The force of interaction acting between two magnetic poles is directly proportional to the product of their pole strengths and inversely proportional to the square of the distance between them.
F = μo / 4π . m1m2 / r2
where m1, m2 = pole strengths, r = distance between poles and μo = permeability of free space.
Magnetic Dipole
Magnetic dipole is an arrangement of two unlike magnetic poles of equal pole strength separated by a very small distance, e.g., a small bar magnet, a magnetic needle, a current carrying loop etc.
Magnetic Dipole Moment
The product of the distance (2 l) between the two poles and the pole strength of either pole is called magnetic dipole moment.
Magnetic dipole moment
M = m (2 l)
Its SI unit is ‘joule/tesla’ or ‘ampere-metre2‘.
Its direction is from south pole towards north pole.
Magnetic Field Due to a Magnetic Dipole
(1) On Axial Line
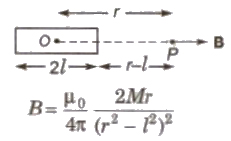
If r > > l, then
B = μo / 4 π 2M / r3
(ii) On Equatorial Line
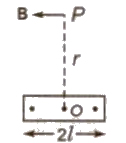
B = μo / 4 π M / (r2 + l2)3 / 2
If r > > l, then
B = μo / 4 π 2M / r3
Torque Acting on a Magnetic Dipole
When a Magnetic Dipole (M) is placed in a uniform magnetic field (B), then a Torque acts on it, Which is given by
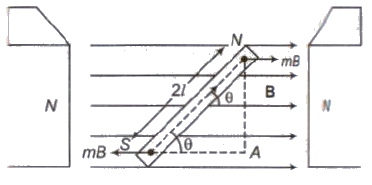
τ = M * B
or τ = MB sin θ
Where θ is angle between the dipole axis and magnetic field.
Potential Energy of a Magnetic Dipole in a Uniform Magnetic Field
The work done in rotating the dipole against the action of the torque is stored as potential energy of the dipole.
Potential Energy, U = W = – MB cos θ = – M . B
Current Carrying Loop
A current carrying loop behaves as a magnetic dipole. If we look the upper face of the loop and current is flowing anti-clockwise,then it has a north polarity and if current is flowing clockwise.then it has a south polarity.
Magnetic dipole moment of a current carrying loop is given by
M = IA
For N such turns M = NIA
Where I = current and A = area of cross-section of the coil.
Gauss’s Law in Magnetism
Surface integral of magnetic field over any closed or open surface is always m.
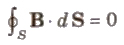
This law tells that the net magnetic flux through any surface is always zero.
[When in an atom any electron revolve in an orbit it is equivalent to a current loop. Therefore, atom behaves as a magnetic dipole].
Magnetic Moment of an Atom
Magnetic moment of an atom M = 1 / 2 eωr2
where e = charge on an electron, ω = angular velocity of electron and r = radius of orbit.
or M = n eh / 4πm
where h = Planck’s constant and m ~ mass of an electron and eh / 4πm = μB, called Bohr magneton and its value is 9.27 * 10-24 A-m2.
Earth’s Magnetism
Earth is a huge magnet. There are three components of earth’s magnetism
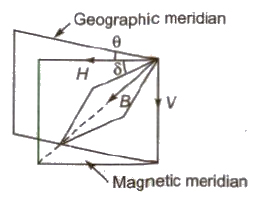
(i) Magnetic Declination (θ) The smaller angle subtended between the magnetic meridian and geographic meridian is called magnetic declination.
(ii) Magnetic Inclination or Magnetic Dip (δ) The smaller angle sub tended between the magnetic axis and horizontal is called magnetic inclination on magnetic dip.
(iii) Horizontal Component of Earth’s Magnetic Field (H) If B is the intensity of earth’s magnetic field then horizontal component of earth’s magnetic field H = B cos δ
It acts from south to north direction.
Vertical component of earth’s magnetic field
V = B sin δ
∴ B = √H2+ V2
and tan δ = V / H
Angle of dip is zero at magnetic equator and 90° at poles.
Magnetic Meridian
A vertical plane passing through the magnetic axis is called magnetic mendian.
Geographic Meridian
A vertical plane passing through the geographic axis is called geographic meridian.
Magnetic Map
Magnetic map is obtained by drawing lines on the surface of earth. which passes through different places having same magnetic elements.
The main lines drawn on earth’s surface are g1 en below
(i) Isogonic Line A line joining places of equal declination is called on isogonic line.
(ii) Agonic Line A line joining places of zero declination is called an agonic line
(iii) Isoclinic Line A line joining places of equal inclination or dip is called an aclinic line,
(iv) Aclinic Line A hne joining places of zero inclination or dip is called an aclinic line.
(v) Isodynamic Line A line joining places of equal horizontal component of earth’s magnetic field (H) is called an isodynamic line.
Magnetic Latitude
(i) If at any place, the angle of dip is δ and magnetic latitude is λ then tan δ = 2 tan λ
(ii) The total Intensity of earth’s magnetic field
I = I0 √1 + 3 sin2 λ
where Io = M / R3
It is assumed that a bar magnet of earth has magnetic moment M and radius of earth is R.
(Magnetic maps are maps obtained by drawing lines passing through different places on the surface of earth, having the same value of a magnetic element.)
Neutral Points
Neutral point of a bar magnet is a point at which the resultant magnetic field of a bar magnet and horizontal component of earth’s magnetic field are zero.
When north pole of a bar magnet is placed towards south pole of the earth. then neutral point is obtained on axial line.
B = μo / 4π 2Mr / (r2 – l2)2 = H
If r > > l, then B = μo / 4π 2M / r3 = H
When north pole of a bar magnet is placed towards north pole of the earth, then neutral point is obtained on equatorial line
B = μo / 4π 2Mr / (r2 + l2)2 = H
If r > > l, then B = μo / 4π 2M / r3 = H
Tangent Law
When a bar magnet is freely suspended under the combined effect of two uniform magnetic fields of intensities B and H acting at 90° to each other, then it bar magnet comes to rest making an angle 0 with the direction of H, then
B = H tan θ
Deflection Magnetometer
It is a device used to determine M and H. Its working is based on tangent law.
Deflection magnetometer can be used into two settings
(i) Tangent A setting In this setting the arms of the magnetometer are along east-west and magnet is parallel to the arms.
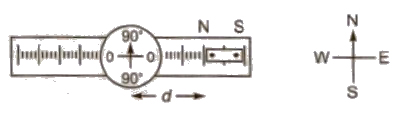
In equilibrium
B = H tan θ
μo / 4π 2M / d3 = H tan θ
(ii) Tangent B setting In this setting the arms of the magnetometer are along north-south and magnet is perpendicular to these arm in equilibrium
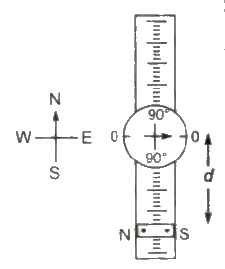
μo / 4π M / d3 = H tan θ
In above setting the experiment can be performed in two ways.
(a) Deflection method In this method one magnet is used at a time and deflection in galvanometer is observed. Ratio of magnetic dipole moments of the magnets
M1 / M2 = tanθ1 / tanθ2
where θ1 and θ2 are mean values of deflection for two magnets.
(b) Null method In this method both magnets are used at a time and no deflection condition is obtained. If Magnets are at distance d1 and d2 then
M1 / M2 = (d1 / d2)3
Tangent Galvanometer
It is a device used for detection and measurement of low electric currents. Its working is based on tangent law. If θ is the deflection produced in galvanometer when I current flows through it, then
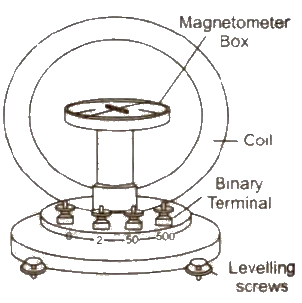
I = 2R / Nμo H tan θ = H / G tan θ = K tan θ
Where G = Nμ / 2R is called galvanometer constant and K = H / G, is called reduction factor of tangent galvanometer.
Here N is number of turns in the coil and R is radius of the coil.
Tangent galvanometer is also called moving magnet type galvanometer.
Vibration Magnetometer
It is based on simple harmonic oscillations of a magnet suspended in uniform magnetic field.
Time period of vibrations is given by
T = 2π √I / MH
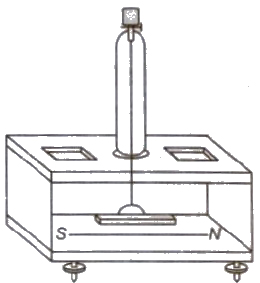
where, I = moment of inertia of the magnet,
M = magnetic dipole moment of the magnet and
H = horizontal component of earth’s magnetic field.
When two magnets of unequal size are placed one above the other and north poles of both magnets are towards geographic north then time period of oscillations is given by
T1 = 2π√I1 + I2 / (M1 + M2) H
If north pole of first magnet and south pole of second magnet is towards geographic north, then time period of oscillations is given by
T2 = 2π√(I1 + I2) / (M1 – M2) H
Then, M1 / M2 = T22 + T21 / T22 – T21
Magnetic Flux
The number of magnetic lines of force passing through any surface is called magnetic flux linked with that surface.
Magnetic flux (phi;) = B . A = BA cos θ
where B is magnetic field intensity or magnetic induction, A is area of the surface.
Its unit is ‘weber’.
Magnetic Induction
The magnetic flux passing through per unit normal area, is called magnetic induction.
Magnetic induction (B) = φ / A
Its unit is ‘waber/metre2‘ or ‘tesla’.
Magnetic of Material
To describe the magnetic properties of materials, following terms are required
(i) Magnetic Permeability It is the ability of a material to permit the passage of magnetic lines of force through it.
Magnetic permeability (μ) = B / H
where B is magnetic induction and H is magnetising force or magnetic intensity.
(ii) Magnetising Force or Magnetic Intensity The degree up to which a magnetic field can magnetise a material is defined in terms of magnetic intensity.
Magnetic intensity (H) = B / μ
(iii) Intensity of Magnetisation The magnetic dipole moment developed per unit volume of the material is called intensity of magnetisation.
Intensity of magnetisation (I) = M / V = m / A
where V = volume and A = area of cross-section of the specimen.
Magnetic induction B = μo (H + I)
(iv) Magnetic Susceptibility(χm) The ratio of the intensity of magnetisation (1) induced in the material to the magnetising force (H) applied, is called magnetic susceptibility.
Magnetic Susceptibility(χm) = I / H
[Relation between Magnetic Permeability and Susceptibility is given by
μ = μo (1 + χm) ]
Classification of Magnetic Materials
On the basis of their magnetic properties magnetic materials are divided into three categories
(i) Diamagnetic substances
(ii) Paramagnetic substances
iii) Ferromagnetic substances
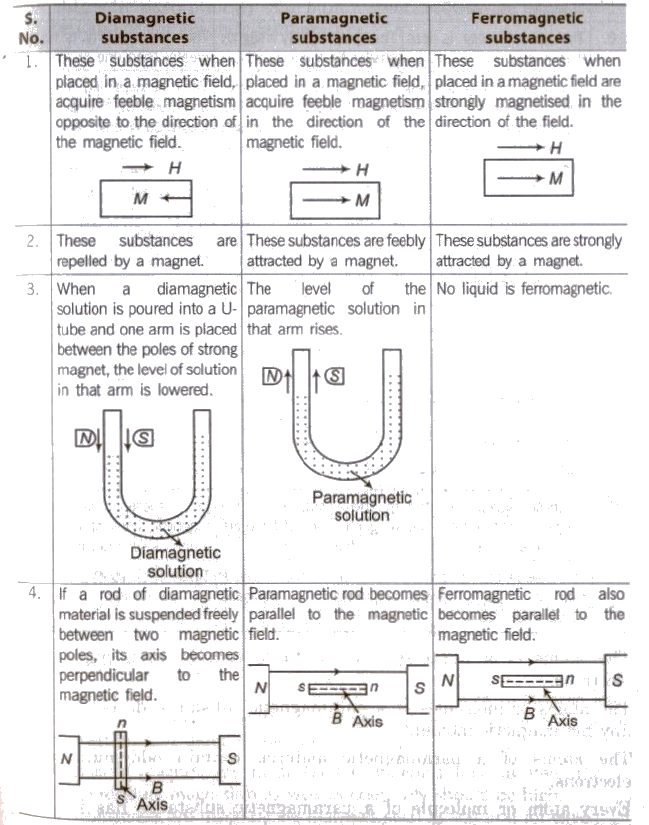

The atoms of a paramagnetic substance contain even number of electrons.
The atoms or molecules of a paramagnetic substance do not possess any net magnetic moment.
The atoms of a paramagnetic material contain odd number of electrons.
Every atom or molecule of a paramagnetic substance has its own magnet moment, i.e., its each atom or molecule is a tiny magnet.
In a ferromagnetic substance, there are several tiny regions called domains. Each domain contain approximately 1010 atoms.
Each domain is a strong magnet as all atoms or molecules in a domain have same direction of magnetic moment.
Curie Law in Magnetism
The magnetic susceptibility of a paramagnetic substance is inversely proportional to its absolute temperature.
χm ∝ 1 / T ⇒ χm T = constant
where χm = magnetic susceptibility of a para magnetic substance and T = absolute temperature.
Hysteresis
The lagging of intensity of magnetisation (I) or magnetic induction (B) behind magnetising field (H), when a specimen of a magnetic substance is taken through a complete cycle of magnetisation is called hysteresis.
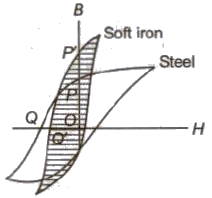
Retentivity or Residual Magnetism
The value of the intensity of magnetisation of a material, when the magnetising field is reduced to zero is called retentivity or residual magnetism of the material.
Coercivity
The value of the reverse magnetising field that should be applied to a given sample in order to reduce its intensity of magnetisation or magnetic induction to zero is called coercivity.
Permanent Magnets
Commonly steel is used to make a permanent magnet because steel has high residual magnetism and high coercivity.
Electromagnets
Electromagnets are made of soft iron because area of hysteresis loop for soft iron is small. Therefore, energy loss is small for a cycle of magnetisation and demagnetisation.
(Permanent magnets are made by the materials such as steel, for which residual magnetism as well as coercivity should be high. Electromagnets are made by the materials such as soft iron for which residual magnetism is high, coercivity is low and hysteresis loss is low).
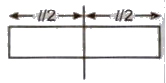
Important Points
(i) Parallel to its length
M’ = m / 2 * l = M / 2

(ii) Perpendicular to its length
M’ = m * l / 2 = M / 2
M’ = m * 2R = m * 2 * 1 / π (πR = I)
= 2M / π (M = m * l)
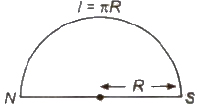
M’ = 2√2M / π
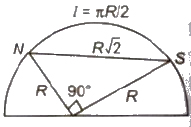
M’ = M / √2
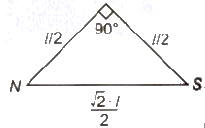
M = 3M / π
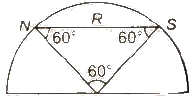
M’ = M / 2
F = K 6M1M2 / d4 in end- on position.
Here,d denotes the separation between magnets.
Others Class 12 Physics Chapters:-










