
Modern Physics Class 12
Modern Physics
Modern physics is a branch of physics that deals with the post-Newtonian concepts in the world of physics.
Cathode Rays
Cathode rays are the stream of fast moving electrons. These rays are produced in a discharge tube at a pressure below 0.01 rom of mercury.
Properties of Cathode Rays
evB = eE or v = E / B
where, E = electric field, B = magnetic field and V = potential difference applied across ends of tube.
Positive Rays
Positive rays were discovered by Goldstein. Positive rays are moving positive ions of gas filled in the discharge tube. The mass of these particles is nearly equal to the mass of the atoms of gas.
Electron Emission
It is the phenomenon of emission of electron from the surface of a metal. The electron emission can be obtained from the following process
Photon
Photons are the packets of energy emitted by a source of radiation. The energy of each photon is,
E = hv
Where h is Planck’s constant and v is frequency of radiation.
Photon travels with speed of light.
The rest mass of a photon is zero.
Photons are electrically neutral.
The momentum of a photon
p = hv / c = h / λ
Dynamic or kinetic mass 0f photon
m = hv / c2 = h / cλ
where c is speed of light in vacuum and λ is wavelength of radiation.
A body can radiate or absorb energy in whose number multiples of a quantum hv, 2hv, 3hv …. nhv, where n is positive integer.
Photoelectric Effect
The phenomena of emission of electrons from a metal surface, when radiations of suitable frequency is incident on it, is called photoelectric effect.
Terms Related to Photoelectric Effect
Relation between work function, threshold frequency and threshold wavelength
φ = hvo = hc / λmax
Laws of Photoelectric Effect
1. For a given metal and frequency of incident light, the photo electric current (the rate of emission of photoelectrons) is directly proportional to the intensity of incident light.
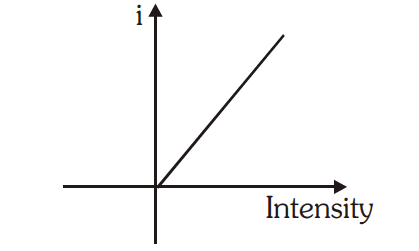
2. For a given metal. there is a certain minimum frequency, called threshold frequency, below which there is no emission of photo electrons takes place.
3. Above threshold frequency the maximum kinetic energy of photo electrons depends upon the frequency of incident light.
4. The photoelectric emission is an instantaneous process.
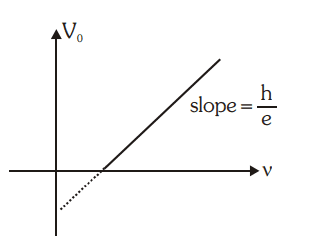
Einstein’s Photoelectric Equation
The maximum kinetic energy of photoelectrons
(Ek)max = hv – φ = h(v – vo)
where v is frequency of incident light and vo is threshold frequency.
Stopping Potential
The minimum negative potential given to anode plate at which photoelectric current becomes zero is called stopping potential (Vo).
Maximum kinetic energy of photo electrons
(Ek)max = 1 / 2 mv2max = eVo
Matter Waves
A wave is associated with every moving particle, called matter or de-Broglie wave.
de-Broglie Wavelength
If a particle of mass m is moving with velocity v, then wavelength of de-Broglie wave associated with it is given by
λ = h / p = h / mv
de-Broglie wavelength of an electron is given by
λ = h / mv = h / √2me V = 12.27 / √V A.
where, m = mass of electron, e = electronic charge and V = potential difference with which electron is accelerated.
Davisson and Germer proves the existence of de-Broglie waves associated with an electron in motion.
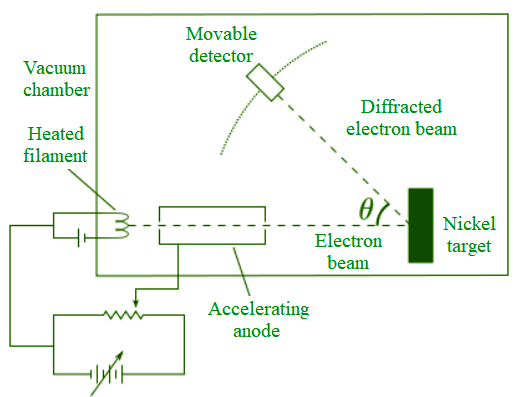
Davisson-Germer Experiment
The wave nature of the material particles as predicted by de-Broglie was confirmed by Davisson and Germer (1927) in united states and by GP Thomson (1928) in scotland.
This experiment verified the wave nature of electron using Ni crystal.
Davisson and Germer found that the intensity of scattered beam of electrons was not the same but different at different angles of scattering. It is maximum for diffracting angle 50° at 54 V potential difference.
Atomic Structure
Dalton’s Atomic Theory
All elements are consists of very small invisible particles, called atoms. Atoms of same element are exactly same and atoms of different element are different.
Thomson’s Atomic Model
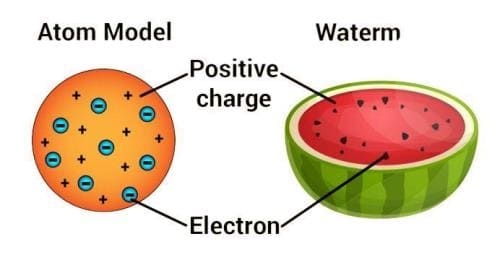
Every atom is uniformly positive charged sphere of radius of the order of 10-10 m, in which entire mass is uniformly distributed and negative charged electrons are embedded randomly. The atom as a whole is neutral.
Limitations of Thomson’s Atomic Model
Rutherford's α-Particle Scattering Experiment
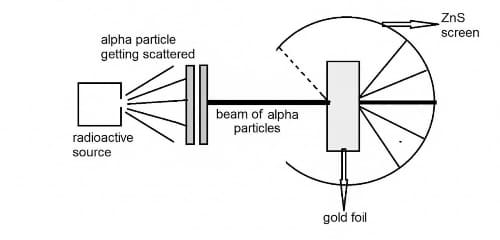
In 1911, Earnest Ruthorford performed a critical experiment that showed that Thomson's model could not be correct. In this experiment a beam of positively charged alpha particles (helium nuclei)
was projected into a thin gold foil. It is observed that most of the alpha particles passed through the foil as if it were empty space. But some surprising results are also seen. Several alpha
particles are deflected from their original direction by large angles. Few alpha particles are observed to be reflected back, reversing their direction of travel.
Rutherford’s Atomic Model
On the basis of this experiment, Rutherford made following observations
Limitations of Rutherford Atomic Model
Bohr’s Atomic Model
Electron can revolve in certain non-radiating orbits called stationary or bits for which the angular momentum of electron is an integer multiple of (h / 2π)
mvr = nh / 2π
where n = I, 2. 3,… called principle quantum number.
The radiation of energy occurs only when any electron jumps from one permitted orbit to another permitted orbit.
Energy of emitted photon
hv = E2 – E1
where E1 and E2are energies of electron in orbits.
Radius of orbit of electron is given by
r = n2h2 / 4π2 mK Ze2 ⇒ r ∝ n2 / Z
where, n = principle quantum number, h = Planck’s constant, m = mass of an electron, K = 1 / 4 π ε, Z = atomic number and e = electronic charge.
Velocity of electron in any orbit is given by
v = 2πKZe2 / nh ⇒ v ∝ Z / n
Frequency of electron in any orbit is given by
v = KZe2 / nhr = 4π2Z2e4mK2 / n3 h3
⇒ v prop; Z3 / n3
Kinetic energy of electron in any orbit is given by
Ek = 2π2me4Z2K2 / n2 h2 = 13.6 Z2 / n2 eV
Potential energy of electron in any orbit is given by
Ep = – 4π2me4Z2K2 / n2 h2 = 27.2 Z2 / n2 eV
⇒ Ep = ∝ Z2 / n2
Total energy of electron in any orbit is given by
E = – 2π2me4Z2K2 / n2 h2 = – 13.6 Z2 / n2 eV
⇒ Ep = ∝ Z2 / n2
Wavelength of radiation emitted in the radiation from orbit n2 to n1 is given by
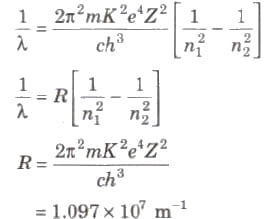
In quantum mechanics, the energies of a system are discrete or quantized. The energy of a particle of mass m is confined to a box of length L can have discrete values of energy given by the relation
En = n2 h2 / 8mL2 ; n < 1, 2, 3,…
Hydrogen Spectrum Series
Each element emits a spectrum of radiation, which is characteristic of the element itself. The spectrum consists of a set of isolated parallel lines and is called the line spectrum.
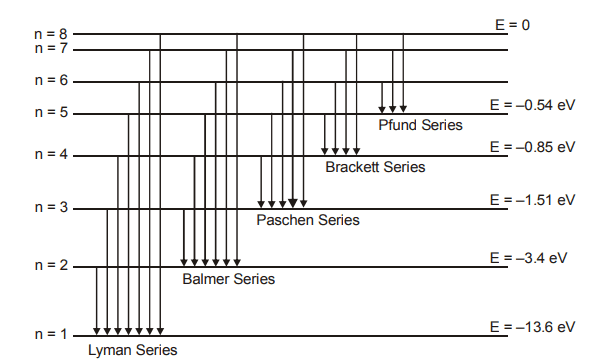
Hydrogen spectrum contains five series
This series lies in ultra violet region.
This series lies in visual region.
This series lies in infrared region
This series lies in infrared region.
This series lies in infrared region.
Wave Model
It is based on wave mechanics. Quantum numbers are the numbers required to completely specify the state of the electrons.
In the presence of strong magnetic field, the four quantum number are
X-Rays
When cathode rays strike on a heavy metal of high melting point. then a very small fraction of its energy converts in to a new type of waves, called X-rays.
Properties of X-rays
X-rays were discovered by Roentgen.
where, h = Planck’s constant, c = speed of light, e = electronic charge and V = potential difference applied across the ends of the tube.
I = Ioe– μx, where Io = initial intensity of X-rays, I = final intensity of emergent X-rays, x = thickness of material and μ = absorption coefficient.
Diffraction of X-rays
X-rays can be diffracted by crystals following Bragg’s law. According to which
2d sin θ = n λ
where, n = 1, 2, 3, …, and d = spacing of crystal planes, θ = angle of diffraction.
X-rays Spectrum
The energy spectrum of X-. rays is a line spectrum, containing following series :
First lines of these series are called Kα, Lα, Mα. Second lines of these series are called Kβ, Lβ, Mβ
Moseley’s Law
The frequency of X-ray is given by
V = a (Z – b)2
where a and b are constants and Z is atomic number of element.
Frequency of X-rays
v ∝ Z2
Compton Effect
When a monochromatic beam of X – falls on a target containing free electrons. it is scattered. As a result, the electrons recoil and scattered radiation has wavelength longer than incident one. This effect is called Compton effect.
(i) λ’ – λ = λ = Compton shift Δλ = h / moc (1 – cos φ) where mo is rest mass of an electron and c is the speed of light h / moc Compton shift Δλ is maximum, when φ = 180°
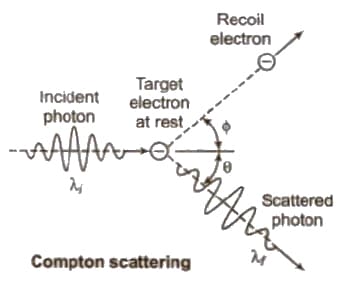
(ii) Kinetic energy of recoil electron
Ek = hc / λ – hc / λ’
(iii) Direction of recoil electron
tan θ = λ sin φ / λ’ – λ cos φ
(iv) Compton wavelength of electron
= h / moc = 0.024 A
(v) Maximum Compton shift
(Δλ)max = 2h / moc 0.0048 A
Nuclear physics
Nucleus
The entire positive charge and nearly the entire mass of atom is concentrated in a very small space called the nucleus of an atom.
The nucleus consists of protons and neutrons. They are called nucleons.
Terms Related to Nucleus
(i) Atomic Number The number of protons in the nucleus of an atom of the element is called atomic number (Z) of the element.
(ii) Mass Number The total number of protons and neutrons present inside the nucleus of an atom of the element is called mass number (A) of the element.
(iii) Nuclear Size The radius of the nucleus R ∝ A1/3
⇒ R = Ro A1/3
where, Ro = 1.1 * 10-15 m is an empirical constant.
(iv) Nuclear Density Nuclear density is independent of mass number and therefore same for all nuclei.
ρ = mass of nucleus / volume of nucleus ⇒ ρ = 3m / 4π R3o
where, m = average mass of a nucleon.
(v) Atomic Mass Unit It is defined as 1 / 12th the mass of carbon nucleus.
It is abbreviated as arnu and often denoted by u. Thus
1 amu = 1.992678 * 10-26 / 12 kg
= 1.6 * 10-27 kg = 931 Me V
Isotopes
The atoms of an element having same atomic number but different mass numbers. are called isotopes.
e.g., 1H1, 1H2, 1H3 are isotopes of hydrogen.
Isobars
The atoms of different elements having same mass numbers but different atomic numbers, are called isobars.
e.g., 1H3, 2He3 and 10Na22, 10Ne22 are isobars.
Isotones
The atoms of different elements having different atomic numbers and different mass numbers but having same number of neutrons, are called isotones.
e.g., 1H3, 2He4 and 6C14, 8O16 are isobars.
Isomers
Atoms having the same mass number and the same atomic number but different radioactive properties are called isomers,
Nuclear Force
The force acting inside the nucleus or acting between nucleons is called nuclear force.
Nuclear forces are the strongest forces in nature.
According to the Yukawa, the nuclear force acts between the nucleon due to continuous exchange of meson particles.
Mass Defect
The difference between the sum of masses of all nucleons (M) mass of the nucleus (m) is called mass defect.
Mass Defect (Δm) = M – m = [Zmp + (A – Z)mn – mn]
Nuclear Binding Energy
The minimum energy required to separate the nucleons up to an infinite distance from the nucleus, is called nuclear binding energy.
Nuclear binding energy per nucleon = Nuclear binding energy / Total number of nucleons
Binding energy, Eb = [Zmp + (A – Z) mn – mN]c2
Packing Fraction (P)
p = (Exact nuclear mass) – (Mass number) / Mass number
= M – A / M
The larger the value of packing friction. greater is the stability of the nucleus.
[The nuclei containing even number of protons and even number of neutrons are most stable.
The nuclei containing odd number of protons and odd number of neutrons are most instable.]
Radioactivity
The phenomena of disintegration of heavy elements into comparatively lighter elements by the emission of radiations is called radioactivity. This phenomena was discovered by Henry Becquerel in 1896.
Radiations Emitted by a Radioactive Element
Three types of radiations emitted by radioactive elements
(i) α-rays
(ii) β-rays
(iii) γ – rays
α-rays consists of α-particles, which are doubly ionised helium ion.
β-rays are consist of fast moving electrons.
γ – rays are electromagnetic rays.
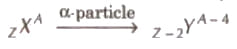
When an α – particle is emitted by a nucleus its atomic number decreases by 2 and mass number decreases by 4.
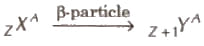
When a β -particle is emitted by a nucleus its atomic number is Increases by one and mass number remains unchanged.
When a γ – particle is emitted by a nucleus its atomic number and mass number remain unchanged
Radioactive Decay law
The rate of disintegration of radioactive atoms at any instant is directly proportional to the number of radioactive atoms present in the sample at that instant.
Rate of disintegration ( – dN / dt) ∝ N
– dN / dt = λ N
where λ is the decay constant.
The number of atoms present undecayed in the sample at any instant N = No e-λt
where, No is number of atoms at time t = 0 and N is number of atoms at time t.
Half-life of a Radioactive Element
The time is which the half number of atoms present initially in any sample decays, is called half-life (T) of that radioactive element.
Relation between half-life and disintegration constant is given by
T = log2e / λ = 0.6931 / λ
Average Life or Mean Life(τ)
Average life or mean life (τ) of a radioactive element is the ratio of total life time of all the atoms and total number of atoms present initially in the sample.
Relation between average life and decay constant τ = 1 / λ
Relation between half-life and average life τ = 1.44 T
The number of atoms left undecayed after n half-lifes is given by
N = No (1 / 2)n = No (1 / 2) t/T
where, n = t / T, here t = total time.
Activity of a Radioactive Element
The activity of a radioactive element is equal to its rate of disintegration.
Activity R = ( – dN / dt)
Activity of the sample after time t,
R = Ro e -λt
Its SI unit is Becquerel (Bq).
Its other units are Curie and Rutherford.
1 Curie = 3.7 * 1010 decay/s
1 Rutherford = 106 decay/s
Nuclear Fission
The process of the splitting of a heavy nucleus into two or more lighter nuclei is called nuclear fission.
When a slow moving neutron strikes with a uranium nucleus (92U235), it splits into 56Ba141 and 36Kr92 along with three neutrons and a lot of energy.
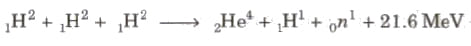
Nuclear Chain Reaction
If the particle starting the nuclear fission reaction is produced as a product and further take part in the nuclear fission reaction, then a chain of fission reaction started, which is called nuclear chain reaction.
Nuclear chain reaction are of two types
(i) Controlled chain reaction
(ii) Uncontrolled chain reaction
Nuclear Reactor
The main parts of a nuclear reactor are following
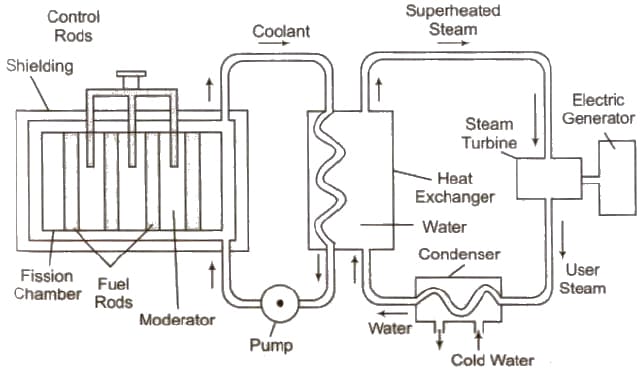
(i) Fuel Fissionable materials like 92U235, 92U238, 94U239 are used as fuel.
(ii) Moderator Heavy water, graphite and beryllium oxide are used to slower down fast moving neutrons.
(iii) Coolant The cold water, liquid oxygen, etc. are used to remove heat generated in the fission process.
(iv) Control rods Cadmium or boron rods are good absorber of neutrons and therefore used to control the fission reaction.
Atom bomb working is based on uncontrolled chain reaction.
Nuclear Fusion
The process of combining of two lighter nuclei to form one heavy nucleus, is called nuclear fusion.
Three deuteron nuclei (1H2) fuse, 21.6 MeV is energy released and nucleus of helium (2He4) is formed.
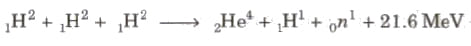
In this process, a large amount of energy is released.
Nuclear fusion takes place at very high temperature approximately about 107 K and at very high pressure 106 atmosphere.
Hydrogen bomb is based on nuclear fusion.
The source of Sun’s energy is the nuclear fusion taking place at sun.
Thermonuclear Energy
The energy released during nuclear fusion is know as thermonuclear energy. Protons are needed for fusion while neutrons are needed for fission process.
Others Class 12 Physics Chapters:-










